By Luc Brogat-Motte, Alessandro Rudi, Céline Brouard, Juho Rousu, Florence d’Alché-Buc.
Submitted to AISTATS, 2021
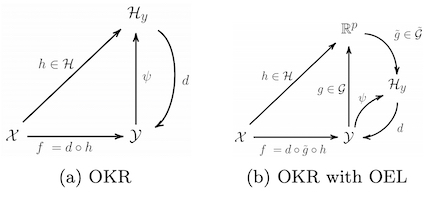
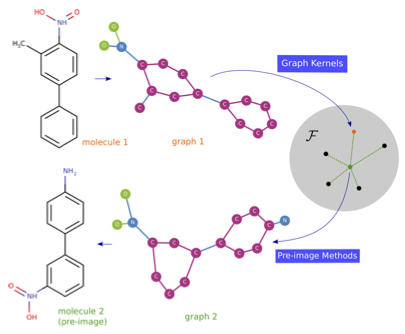
Abstract. A powerful and flexible approach to structured prediction consists in embedding the structured objects to be predicted into a feature space of possibly infinite dimension by means of output kernels, and then, solving a regression problem in this output space. A prediction in the original space is computed by solving a pre-image problem. In such an approach, the embedding, linked to the target loss, is defined prior to the learning phase. In this work, we propose to jointly learn a finite approximation of the output embedding and the regression function into the new feature space. For that purpose, we leverage a priori information on the outputs and also unexploited unsupervised output data, which are both often available in structured prediction problems. We prove that the resulting structured predictor is a consistent estimator, and derive an excess risk bound. Moreover, the novel structured prediction tool enjoys a significantly smaller computational complexity than former output kernel methods. The approach empirically tested on various structured prediction problems reveals to be versatile and able to handle large datasets.